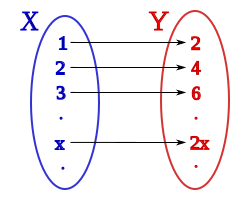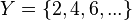Definición
Una función puede considerarse como un caso particular de una
relación o de
correspondencia matemática. Cada relación o correspondencia de un elemento

con un (y sólo un)

se denota

, en lugar de
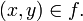
Formalmente, pedimos que se cumplan las siguientes dos condiciones:
- Condición de existencia: Todos los elementos de X están relacionados con elementos de Y, es decir,
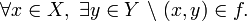
- Condición de unicidad: Cada elemento de X está relacionado con un único elemento de Y, es decir, si

|
Notación y nomenclatura
Al dominio también se le llama
conjunto de entrada o
conjunto inicial. Se denota por

o

. A los elementos del dominio se les llama habitualmente
argumento de la función.
Al codominio, también llamado,
conjunto de llegada,
conjunto final o
rango de
f se le denota por
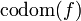 o codomf
o codomf
Cabe señalar que el término
rango es ambiguo en la literatura, ya que puede hacer referencia tanto al codominio como al conjunto imagen. Por ello, es aconsejable usar el término codominio.
Si
x es un elemento del dominio al elemento del codominio asignado por la función y denotado por
f(x) se le llama
valor o
imagen de la función
f de
x. Al subconjunto del codominio formado por todos los valores o imágenes se le llama
imagen,
alcance o
recorrido de la función. Se denota por

o

o
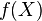
.
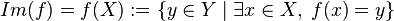
Una
preimagen de un

es algún

tal que

.
Note que puede haber algunos elementos del codominio que no sean imagen de un elemento del dominio, pero que cada elemento del dominio es preimagen de al menos un elemento del codominio.
Ejemplos
- La función definida por
 , tiene como dominio, codominio e imagen a todos los números reales
, tiene como dominio, codominio e imagen a todos los números reales 

Función con Dominio X y Rango Y
- Para la función
 tal que
tal que  , en cambio, si bien su dominio y codominio son iguales a
, en cambio, si bien su dominio y codominio son iguales a  , sólo tendrá como imagen los valores comprendidos entre 0 y +∞.
, sólo tendrá como imagen los valores comprendidos entre 0 y +∞.
- En la figura se puede apreciar una función
 , con
, con

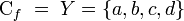
- Note que a cada elemento de X le corresponde un único elemento de Y. Además, el elemento a de Y no tiene origen, y el elemento b tiene dos (el 1 y el 4). Finalmente,

- Esta función representada como relación, queda:

Igualdad de funciones
Sean las funciones
f: A → B y
g: C → D, decimos que
f es igual a g y escribimos
f=g si y sólo si se cumple que ambas funciones:
- tienen igual dominio, A=C,
- tienen igual codomino, B=D, y
- tiene la misma asignación, es decir que para cada x se cumple que f(x)=g(x).
Representación de funciones
Las funciones se pueden presentar de distintas maneras:
- usando una relación matemática descrita mediante una expresión matemática: ecuaciones de la forma y = f(x). Cuando la relación es funcional, es decir satisface la segunda condición de la definición de función, se puede definir una función que se dice definida por la relación, A menos que se indique lo contrario, se supone en tales casos que el dominio es el mayor posible (respecto a inclusión) y que el codominio son todos los Reales. El dominio seleccionado se llama el dominio natural, de la función.
- Ejemplo: y=x+2. Dominio natural es todos los reales.
- Ejemplo: "Para todo x, número entero, y vale x más dos unidades".
- Como tabulación: tabla que permite representar algunos valores discretos de la función.
- Ejemplo:
X| -2 -1 0 1 2 3
Y| 0 1 2 3 4 5
- Ejemplo: A={(-2, 0),(-1, 1),(0, 2),(1, 3), ... (x, x+2)}
- Ejemplo:
| 5 | | | | | | X |
| 4 | | | | | X | |
| 3 | | | | X | | |
| 2 | | | X | | | |
| 1 | | X | | | | |
| 0 | X | | | | | |
| y / x | -2 | -1 | 0 | 1 | 2 | 3 |
Clasificación de las funciones
Dados dos conjuntos
X,
Y, consideremos a todas las posibles aplicaciones (funciones) que pueden formarse entre estos dos conjuntos. Podemos diferenciar los siguientes casos:
- Si a cada imagen le corresponde una única preimagen, inyectiva.
- Si la imagen de la función es igual al codominio, sobreyectiva o suprayectiva.
- Una función que sea inyectiva y sobreyectiva simultáneamente, se denomina biyectiva .
Puede haber funciones que sean biyectivas, inyectivas pero no suprayectivas, supreyectiva pero no inyectiva o que no se cumple ninguna de esas condiciones, en cuyo caso no tiene un nombre específico.
'
Definiciones alternas: sea

dada y sea
b un elemento cualquiera del codominio
Y. Consideremos la ecuación
 .
.
- la función es suprayectiva o sobreyectiva si, y sólo si, la ecuación (*) siempre tiene al menos una solución.
- la función es inyectiva si, y sólo si, la ecuación (*) tiene a lo más una solución.
- la función es biyectiva cuando, y sólo cuando, es inyectiva y suprayectiva a la vez.
Vamos a ilustrar esos diferentes tipos de funciones (aplicaciones) en un
Diagrama de Venn, el conjunto universal
U, representado por un rectángulo, es el conjunto de todas las posibles aplicaciones, el conjunto
A es aquel de las aplicaciones inyectivas, y el conjunto
B aquel de las sobreyectivas, esto nos permite ver los distintos tipos de aplicaciones de un modo gráfico.
Aplicación inyectiva y no sobreyectiva
En una función inyectiva, cada elemento imagen tiene única preimágen. Un función que no sea inyectiva, tendrá al menos dos elementos diferentes del dominio que tienen la misma imagen.
En una función suprayectiva (sobreyectiva) cada elemento del codominio es imagen de algún elemento del dominio. Una función no será suprayectiva, cuando al menos un elemento del codominio (conjunto final) no tenga una preimagen.
En el diagrama de Venn corresponden a las aplicaciones que pertenecen a
A y no pertenecen a
B, esto es las que pertenecen a la diferencia de
A y
B:
A-B.
En estas aplicaciones la cardinalidad de
X es siempre menor que la de
Y, esto es el conjunto
Y tendrá mayor número de elementos que
X cuando tratamos de compararlos.
Ejemplo
en el diagrama de la figura:
- todos los elementos de Y, que tienen origen, tienen un único origen, esto hace que la aplicación sea inyectiva
- el elemento d de Y, no tiene ningún origen por lo que esta aplicación no es sobreyectiva.
Segundo ejemplo
Partiendo del conjunto de pinceles con pintura de colores:
Sobre el conjunto de caras pintadas:
Asociando cada pincel con la cara correspondiente:

Dado que cada pincel tiene una cara y solo una cara de su color esta correspondencia es una aplicación, como las caras que tiene pincel de su color, tienen un solo pincel de su color, la aplicación es inyectiva, y como la cara pintada de amarillo, no tiene ningún pincel de este color, la aplicación no es sobreyectiva.
Aplicación no inyectiva y sobreyectiva
Una aplicación no inyectiva tiene al menos un elemento imagen que tiene dos o más orígenes y una sobreyectiva todos los elementos del conjunto final tienen al menos un elemento origen.
En el diagrama de Venn corresponden a las aplicaciones que no pertenecen a
A y si pertenecen a
B, esto es las que pertenecen a la diferencia de
B y
A:
B-A.
Para esta aplicación el conjunto
X ha de tener mayor número de elementos que
Y, la cardinalidad de
X ha de ser mayor que la de
Y.
Ejemplo
en el diagrama de la figura:
- el elemento c de Y, tiene dos orígenes: el 3 y el 4, por lo que esta aplicación no es inyectiva.
- todos los elementos de Y, tienen origen, esto hace que la aplicación sea sobreyectiva.
Segundo ejemplo
Igual que en el ejemplo anterior partiremos del conjunto de pinceles con pintura de colores:
En este caso hay dos pinceles con pintura azul, pero a pasar de tener el mismo color de pintura son dos pinceles distintos.
Como conjunto final tenemos el conjunto de caras pintadas:
Asociando cada pincel con la cara del mismo color, vemos que cada pincel tiene una cara pintada de su color y solo una, esto hace que la correspondencia sea una aplicación, la cara azul tiene dos pinceles de su mismo color, por lo que no es inyectiva, todas las caras tiene un pincel con su color, luego la aplicación es sobreyectiva.
Aplicación inyectiva y sobreyectiva (biyectiva)
Si una aplicación es inyectiva y sobreyectiva simultáneamente, se denomina biyectiva. Por ser inyectiva los elementos que tienen origen tienen un único origen y por ser sobreyectiva todos los elementos del conjunto final tienen origen.
En el diagrama de Venn el conjunto
A es el de las aplicaciones inyectiva y el conjunto
B el de las aplicaciones sobreyectiva, las aplicaciones biyectiva, que son inyectiva y sobreyectiva, será la intersección de
A y
B.
Estas dos circunstancias dan lugar a que el conjunto
X e
Y tengan el mismo número de elementos, la cardinalidad de
X es la misma que la de
Y, esto tiene una gran importancia cuando se pretende comparar dos conjuntos:
- Si dados dos conjuntos podemos encontrar una aplicación biyectiva entre ellos, podemos afirmar, que los dos conjuntos tienen el mismo número de elementos. La cardinalidad de X es igual a la de Y.
Ejemplo
en el diagrama de la figura:
- todos los elementos de Y, que tienen origen, tienen un único origen, esto hace que la aplicación sea inyectiva
- todos los elementos de Y, tienen origen, esto hace que la aplicación sea sobreyectiva.
Si tomaremos por conjunto inicial el conjunto de los números naturales:

y por conjunto final el de los números naturales pares:
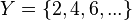
Podemos ver que la relación


Por el que a cada número natural
x de
X, le asociamos un número par
2x de
Y, se cumple:
- f: es una aplicación, dado que a cada uno de los valores x de X le corresponde un único valor 2x de Y.
- esta aplicación es inyectiva dado que a cada número par 2x de Y le corresponde un único valor x de X.
- y es sobreyectiva porque todos los números pares tienen un origen
Esto nos permite afirmar que hay el mismo número de números naturales que de números naturales pares, se da la paradoja de que los números naturales pares en un subconjunto propio de los números naturales, esta circunstancia solo se da con los conjuntos infinitos.
Segundo ejemplo
Tomando el conjunto de pinceles como conjunto inicial:
y el de caras como conjunto final:
La correspondencia que asocia cada pincel con la cara de su mismo color es una aplicación porque todos los pinceles tienen una cara con su color y solo una cara de ese color, la aplicación es inyectiva porque un pincel corresponde con una sola cara, y es sobreyectiva porque todas las caras tiene un pincel de su color, al ser inyectiva y sobreyectiva simultáneamente esta aplicación es biyectiva.
Una aplicación biyectiva hace corresponder los elementos del conjunto inicial con los del conjunto final uno a uno, pudiéndose decir que hay el mismo número de elementos en el conjunto inicial que en el final.
Aplicación no inyectiva y no sobreyectiva
Una aplicación no inyectiva tendrá al menos un elemento imagen que tenga dos o más orígenes y una no sobreyectiva tendrá al menos un elemento del conjunto final que no tenga elemento origen. Este tipo de aplicaciones no tiene un nombre específico y quizá sean las que presenten, desde el punto de vista matemático, un menor interés.
Para esta aplicación los conjuntos
X e
Y no son comparables, y no podemos plantear ningún supuesto sobre su cardinalidad, partiendo de su comparación, ni sobre su número de elementos.
En el diagrama de Venn corresponden a las aplicaciones que no pertenecen a
A y no pertenecen a
B, esto es las que no pertenecen a la unión de
A y
B.
Ejemplo
en el diagrama de la figura:
- el elemento b de Y, tiene dos orígenes: 1 y 2, esto hace que esta aplicación no sea
 con un (y sólo un)
con un (y sólo un)  se denota
se denota  , en lugar de
, en lugar de 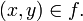
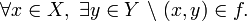

 o
o  . A los elementos del dominio se les llama habitualmente argumento de la función.
. A los elementos del dominio se les llama habitualmente argumento de la función.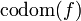 o
o  o
o  o
o 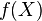 .
.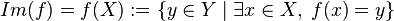
 , tiene como dominio, codominio e imagen a todos los
, tiene como dominio, codominio e imagen a todos los 

 tal que
tal que  , en cambio, si bien su dominio y codominio son iguales a
, en cambio, si bien su dominio y codominio son iguales a  , sólo tendrá como imagen los valores comprendidos entre 0 y +
, sólo tendrá como imagen los valores comprendidos entre 0 y + , con
, con 
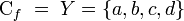



 dada y sea b un elemento cualquiera del codominio Y. Consideremos la ecuación
dada y sea b un elemento cualquiera del codominio Y. Consideremos la ecuación .
.